예제 1)
G(s)=s3+7s2+20s+603s+60이 시스템은 단위계단응답 37.5%의 오버슈트와 4.3초의 정정시간을 가진다. 이 시스템이 오버슈트가 9.48%, 정정시간 1초이하되도록 제어기를 설계하여라.
답)
- 플랜트의 오버슈트와 정정시간을 확인 - 오버슈트 37.5%, 정정시간 4.3초
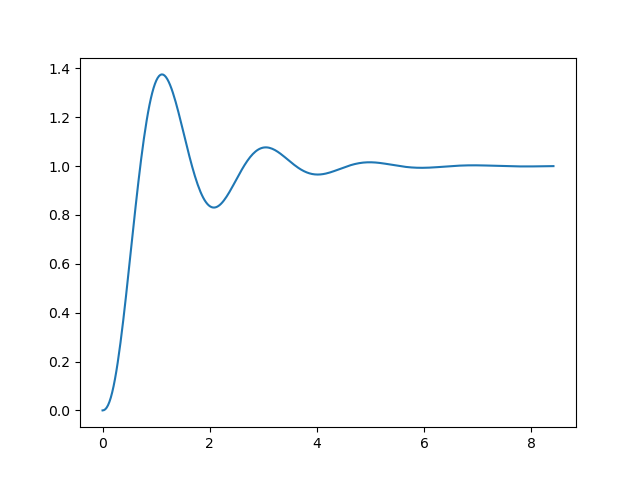
오버슈트 9.48%와 정정시간 1초가 되는 시스템이 되는 a와ω을 구한다.
a=0.6,ω=6.67
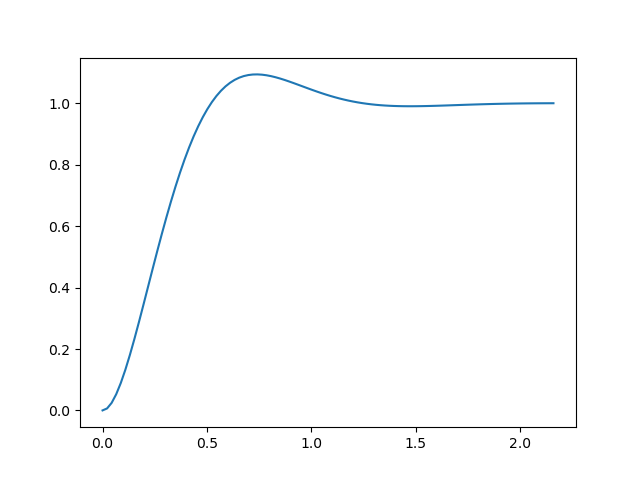
위 시스템의 극점 : −4±j5.334
α(s)에 하나의 극점을 추가 -> 플랜트가 3차이기 때문임
α(s)=(s+4+j5.334)(s+4−j5.334)(s+10∗(4))
액커만 공식을 이용하여 K값을 구한다. K=[−41,34.45,17.18]
새로운 시스템은 Gn=StateSpace(A−B∗K,B,C,D)
Gn=∣Gn∣Gn
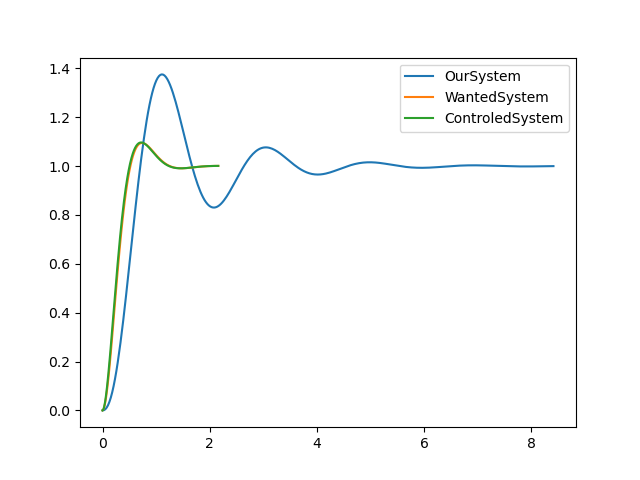
예제 2)
다음 시스템의 백분율 오버슈트 4.3%, 정정시간 1초가 되도록 제어기를 설계하여라.
[x1˙x2˙]=[−301−1][x1x2]+[01]u
y=[1.50.5][x1x2]
답)
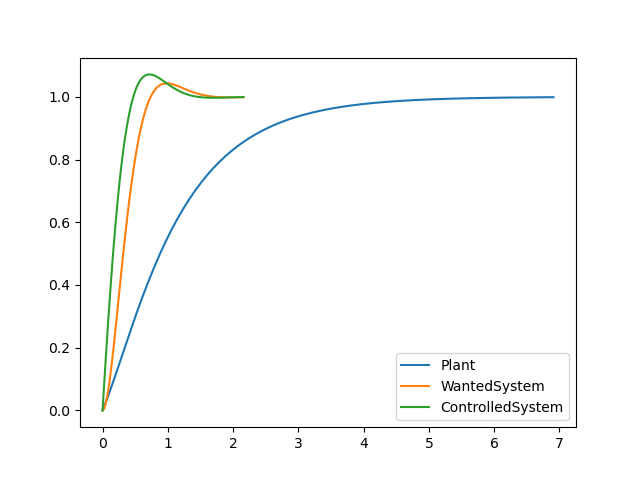
예제 3)
[x1˙x2˙]=[−41−30][x1x2]+[10]u
y=[0.53][x1x2]
s2+8s+32가 되도록 상태부귀환 이득벡터를 구하라.
답)
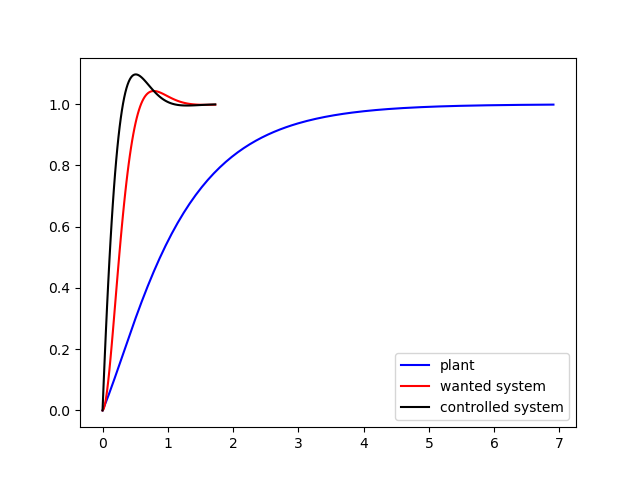
예제 4)
다음 시스템의 오버슈트가 10%, 정정시간 0.8초이하가 되도록 제어기를 설계하여라.
G(s)=s3+10s2+18s+16s2+10s+16





로그인 하면 댓글을 쓸 수 있습니다.