ClassNorm

z-역변환

Z[r(t)]로부터 r(t)를 구하는 방법은

Z[r(t)]의 분자항을 분모항으로 나눠서 급수 형태로 만들 수 있다.

예) $Z[r(t)] = \dfrac{z+1}{z^2+2z+2} = \dfrac{z^{-1}+z^{-2}}{1 +2z^{-1}+2z^{-2}}$

$\tag{1} R(z) = 1z^{-1} -1z^{-2} +0z^{-3} +2z^{-4}+ \cdots$

식(1)의 분모를 분자로 나누어 얻은 결과이다. R(z)의 원하는 부분까지 계산될 수 있다.

$R(z) = \sum_{k =0 }^{\infty}r(kT)z^{-k}$

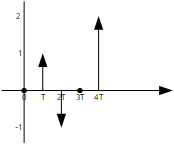
이경우, $R(0) = 0, R(T) = 1, R(2T) = -1, R(3T)=0, R(4T)=2 \cdots$ 와 같이 y(kT)를 얻을 수 있다.

다음 식(2)의 역변화을 부분 분수법으로 전개한다.

$\tag{2} R(z) = \dfrac{z+1}{(z-1)(z-2)}$

역변환을 용이하게 하기 위해 $R(z)$ 를 z로 나눈 후 부분 분수로 전개한다.

$\dfrac{R(z)}{z} = \dfrac{z+1}{z(z-1)(z-2)}$

이를 다음과 같이 부분 분수로 분해할 수 있다.

$\dfrac{z+1}{z(z-1)(z-2)} = \dfrac{A}{z} + \dfrac{B}{z-1} + \dfrac{C}{z-2}$

계수 A, B, C를 구하면

$A = \lim_{z \to 0} { \dfrac{z+1}{(z-1)(z-2)}} = \dfrac{1}{2}$

$B = \lim_{z \to 1} { \dfrac{z+1}{z(z-2)}} = -2$

$C = \lim_{z \to 2} { \dfrac{z+1}{z(z-1)}} = \dfrac{3}{2}$

위에서 구한 계수들을 다시 원래의 식에 대입한다.

$\dfrac{R(z)}{z} = \dfrac{1/2}{z} - \dfrac{2}{z-1} + \dfrac{3/2}{z-2}$

양변에 z를 곱하여 $R(z)$ 를 구한다.

$R(z) = \dfrac{1}{2} - \dfrac{2z}{z-1} + \dfrac{3z}{2(z-2)}$

이제 각 항에 대해 z-변환표를 사용하여 역변환을 적용한다.

$\tag{3} Z^{-1} \left[ \dfrac{z}{z-a} \right] = a^{k}u[kT]$

$\tag{4} Z^{-1} \left[ C \right] = C \delta [kT]$

식(3), (4)을 이용하여 각 항을 역변환하면 다음과 같다.

$\tag{5} Z^{-1} \left[ \dfrac{1}{2} \right] = \dfrac{1}{2} \delta [kT]$

$\tag{6} Z^{-1} \left[ \dfrac{2z}{z-1} \right] = 2 (1)^k u[kT]$

$\tag{7} Z^{-1} \left[ \dfrac{3z}{2(z-2)} \right] = \dfrac{3}{2} (2)^k u[kT]$

식(5), (6), (7)의 모든 항을 합치면 최종 역변환 값 $R(kT)$ 은 다음과 같다.

$r(kT) = \dfrac{1}{2} \delta (kT) -2 u(kT) + \dfrac{3}{2} 2^{k}u(kT)$

여기서 $\delta(kT)$ 는 $k=0$ 일 때만 1의 값을 가지므로, $k \ge 0$ 인 모든 시퀀스를 포함하는 $u(kT)$ 으로 식을 정리하면

$r(kT) = \left( \dfrac{3}{2} 2^{k}-2 \right) u(kT)$

$k=0$ 일 때, $r(0) = \dfrac{1}{2} \cdot 1 - 2 \cdot 1 + \dfrac{3}{2} \cdot 1 = 0$ 이므로 두 식은 동일한 결과를 나타낸다.